Das Tabellenkalkulationsprogramm Excel bietet viele Möglichkeiten mathematische Formeln zu berechnen. Auch Dreisatzformeln lassen sich schnell und einfach in Excel integrieren. Wir zeigen euch in diesem Artikel, wie ihr das umsetzt.
Excel Dreisatz: Wofür benötigt man den Dreisatz?
Der Dreisatz ist eines der wichtigsten mathematischen Lösungsverfahren. Mit ihm können Aufgaben gelöst werden, die zwei Größen proportional oder antiproportional zueinander stehen. Der Begriff Dreisatz bezieht sich auf die drei Rechenschritte, die die Formel voraussetzt.
Worauf muss beim Dreisatz geachtet werden?
Der Dreisatz lässt sich in proportionale und antiproportionale Zuordnungen unterteilen. Die Proportionale Zuordnung wird benötigt, wenn eine Größe X mit einer anderen Menge oder Größe Y verglichen wird und beide Größen proportional zueinander wachsen.
Wenn ihr also berechnen möchtet, wie viel zehn Äpfel kosten, ihr aber den Preis für drei Äpfel wisst, könnt ihr mit dem Dreisatz den Preis berechnen.
Die antiproportionale Zuordnung verhält sich entsprechend andersherum. Hier verhalten sich die Mengen und Größen antiproportional zueinander. Während die Größe X steigt sollte die Menge oder Größe Y sinken. Dazu zeigen wir euch die Beispiele direkt in Excel.
Der Dreisatz in Excel - So geht ihr vor
Erstellt zunächst eine neue Tabelle in Excel. Tragt in die Felder die Bezeichnungen für eure Werte ein, sowie die bekannten Zahlen, die ihr mit der Dreisatz-Formel berechnen möchtet.
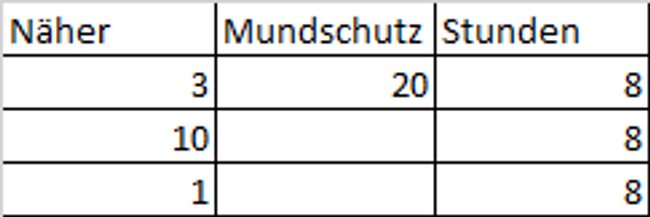
In diesem Beispiel möchtet ihr herausfinden wie viele Mundschutzmasken eine bestimmte Menge Näher in acht Stunden herstellen können. Ihr wisst bereits, dass ein Näher 20 Masken in acht Stunden herstellen kann. Nun geht ihr wie folgt vor:
- Wechselt in das dritte Feld in der Spalte Mundschutz.
- Nun muss die Formel mit den korrekten Variablen eingetragen werden: "=B2/A2*A3"
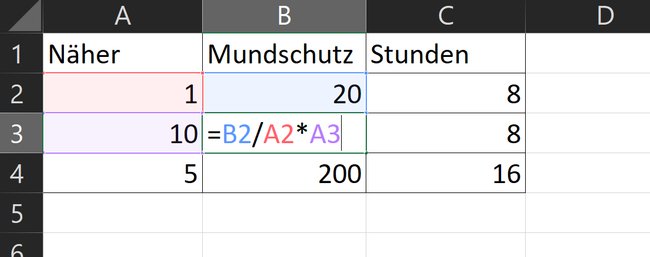
Wir teilen also den Wert 20 Mundschutz durch die Menge der Näher 1, der sie herstellt und multiplizieren das Ergebnis mit der Menge Näher, die wir stattdessen Nutzen möchten 10.
Das gleiche Beispiel lässt sich auch antiproportional berechnen, indem man die Zeit verändert. Wir möchten also herausfinden, wie viele Masken eine bestimmte Zahl Näher in X Stunden herstellen können.
Wir wissen bereits, dass zehn Näher etwa 200 Masken in acht Stunden herstellen können. Wir möchten nun wissen, wie viele Mundschutze die Hälfte an Nähern in 16 Stunden herstellen könnten.
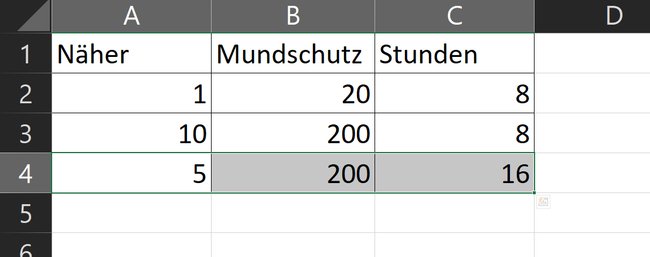
Es zeigt sich, dass die Hälfte der Näher die doppelte Zeit für die gleiche Menge Mundschutz benötigen würden. Hier rechnet ihr die Menge Näher durch zwei und multipliziert die Zeit (antiproportional) mal zwei.